การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย(Simpleharmonic Motion)

การเคลื่อนที่ของสิ่งต่างๆ
เช่น การแกว่งชิงช้า การแกว่งของลูกตุ้ม
การเคลื่อนที่ของมวลที่ติดกับปลายแผ่นสปริง
การเคลื่อนที่ขึ้นลงของผิวน้ำขณะเกิดคลื่นผิวน้ำ
การเคลื่อนที่ของสิ่งเหล่านี้แตกต่างจากการเคลื่อนที่แบบอื่นอย่างไร
การเคลื่อนที่ของชิงช้า
ลูกตุ้มและมวลที่ปลายแผ่นสปริงมีลักษณะที่เหมือนกัน คือ
ถ้าเราเริ่มสังเกตวัตถุดังกล่าวจะเคลื่อนที่ผ่านตำแหน่งสมดุลไปในทิศทางหนึ่งและอัตราเร็วจะลดลงเรื่อยๆจนหยุด
แล้วเคลื่อนที่ย้อนกลับมาตามแนวทางเดิม โดยอัตราเร็วเพิ่มขึ้นเรื่อยๆและมีอัตราเร็วสูงสุดเมื่อผ่านตำแหน่งสมดุล
จากนั้นอัตราเร็วจะลดลงจนหยุดอีกครั้งหนึ่ง
การเคลื่อนที่ของวัตถุติดสปริงบนพื้นราบ
ในรูป วางมวลไว้บนพื้นราบ ผูกวัตถุเข้ากับปลายหนึ่งของสปริงโดยที่อีกปลายหนึ่งของสปริงผูกติดกับผนัง วัตถุจะอยู่นิ่งๆ บนพื้นในตำแหน่งสมดุล เมื่อดึงวัตถุออกจากตำแหน่งสมดุลแล้วปล่อยให้วัตถุเคลื่อนที่บนพื้นราบ วัตถุจะเคลื่อนที่กลับไปกลับมาผ่านตำแหน่งสมดุลและซ้ำเส้นทางเดิมการเคลื่อนที่ในลักษณะนี้มีจำนวนมาก เช่น การสั่นของสายไวโอลินเมื่อถูกสี การสั่นของกลองเมื่อถูกตี การเคลื่อนที่ของวัตถุที่ติดปลายลวดสปริง การเคลื่อนที่ของโมเลกุลอากาศเมื่อเคลื่อนเสียงส่งผ่าน การเคลื่อนที่ของอิเล็กตรอนในสายอากาศของเครื่องส่งวิทยุ เป็นต้น ปริมาณที่สำคัญอย่างหนึ่งของการเคลื่อนที่ในลักษณะนี้ คือ ความถี่ ซึ่งหมายถึงจำนวนรอบของการเคลื่อนที่ใน 1 วินาที แทนสัญลักษณ์ f มีหน่วยเป็นเฮิรตซ์ (Hz) ซึ่ง 1 Hz =

ความถี่จะเป็นส่วนกลับกับคาบ ดังสมการ (4.13) คาบคือ เวลาในการเคลื่อนที่ครบ 1 รอบ ใช้สัญลักษณ์ T แทนคาบ คาบมีหน่วยเป็นวินาที (s)
 (4.13)
(4.13)การเคลื่อนที่ใดๆ ซึ่งเคลื่อนที่กลับไปมาซ้ำทางเดิม โดยผ่านตำแหน่งสมดุลและคาบของการเคลื่อนที่คงตัว ดังแสดงด้วยกราฟของการเคลื่อนที่ในแนวแกน x ดังรูป 4.24 เรียกว่า การเคลื่อนที่แบบพีริออดิก(periodic motion)
กราฟของการเคลื่อนที่แบบพีริออดิก ทางแกน x
การเคลื่อนที่แบบพีริออดิกชนิดหนึ่งที่กราฟของการกระจัดกับเวลาอยู่ในรูปของฟังก์ชันไซน์หรือโคไซน์ความถี่คงที่มีค่าที่แน่นอนค่าเดียว เรียกว่า การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย (simple harmonic motion) นั่นคือ การเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเป็นการเคลื่อนที่แบบพีริออดิกอย่างหนึ่ง อาจจะเรียกย่อๆ ว่า การเคลื่อนที่แบบ SHM การกระจัดทาง x ในรูปฟังก์ชันของเวลา t ของ SHM โดยทั่วไปเขียนเป็นสมการได้เป็น
 (4.14)
(4.14) ซึ่ง
 ,
,  และ
และ เป็นค่าคงตัว
เป็นค่าคงตัว เป็นการกระจัดสูงสุด เรียกว่า แอมพลิจูด (Amplitude)
เป็นการกระจัดสูงสุด เรียกว่า แอมพลิจูด (Amplitude)  เป็นความถี่เชิงมุม มีค่าเท่ากับ
เป็นความถี่เชิงมุม มีค่าเท่ากับ  เมื่อ f เป็นความถี่ หรือเท่ากับ
เมื่อ f เป็นความถี่ หรือเท่ากับ เมื่อ T เป็น คาบ (period)
เมื่อ T เป็น คาบ (period)  เป็นค่าคงตัวทางเฟส (phase constant) หมายถึงเฟสเริ่มต้น คือค่าเฟสที่เวลาเป็นศูนย์ การเคลื่อนที่จะเป็นรูปไซน์หรือโคไซน์ขึ้นกับค่านี้ ถ้า
เป็นค่าคงตัวทางเฟส (phase constant) หมายถึงเฟสเริ่มต้น คือค่าเฟสที่เวลาเป็นศูนย์ การเคลื่อนที่จะเป็นรูปไซน์หรือโคไซน์ขึ้นกับค่านี้ ถ้า  ก็เป็นรูปโคไซน์ ถ้า
ก็เป็นรูปโคไซน์ ถ้า  ก็เป็นรูปไซน์ เนื่องจากรูปโคไซน์และรูปไซน์ต่างกันที่เฟสเท่านั้น จึงอาจเรียกรวมว่าเป็นฟังก์ชันรูปไซน์ (sinusoidal function)
ก็เป็นรูปไซน์ เนื่องจากรูปโคไซน์และรูปไซน์ต่างกันที่เฟสเท่านั้น จึงอาจเรียกรวมว่าเป็นฟังก์ชันรูปไซน์ (sinusoidal function)  ในสมการ (4.14) นับเป็นเฟสที่เปลี่ยนไปตามเวลาของการเคลื่อนที่
ในสมการ (4.14) นับเป็นเฟสที่เปลี่ยนไปตามเวลาของการเคลื่อนที่จากสมการ (4.14) เมื่อเขียนกราฟระหว่างการกระจัดกับเวลา โดยมี
 ต่างๆ กันการกระจัดที่ตำแหน่งเริ่มต้นจะมีค่าขึ้นกับมุมเฟสเริ่มต้น
ต่างๆ กันการกระจัดที่ตำแหน่งเริ่มต้นจะมีค่าขึ้นกับมุมเฟสเริ่มต้น  ดังรูป
ดังรูป 
กราฟระหว่างการกระจัดกับเวลาของฟังก์ชันรูปไซน์  และ
และ </b>
</b>
 และ
และ </b>
</b>
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย จึงอาจจะเขียนได้ในรูป
 (4.15)
(4.15)
ถ้าอนุภาคเริ่มต้นเคลื่อนที่จากตำแหน่งสมดุล (x = 0) ซึ่งจะมีลักษณะเช่นเดียวกับกราฟของ

สรุปได้ว่า สำหรับ การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย คือการเคลื่อนที่ซึ่งมีการกระจัดเป็นฟังก์ชันของเวลาเป็นฟังก์ชันรูปไซน์
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายเทียบกับการเคลื่อนที่เป็นวงกลม
การเคลื่อนที่แบบซิมเปิ้ลฮาร์มอนิก
มีลักษณะคล้ายกับการเคลื่อนที่แบบวงกลม กล่าวคือ
มีการเคลื่อนที่กลับไปกลับมาซ้ำรอยเดิม เมื่อการเคลื่อนที่ครบรอบ ดังนั้น
การศึกษาปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบซิมเปิ้ลฮาร์มอกนิก จึงสามารถศึกษาได้จาก
เงาของวัตถุที่เคลื่อนที่แบบวงกลมในระนาบดิ่ง ที่ตกกระทบไปยังระนาบในแนวดิ่ง
และในแนวระดับ ดังภาพ
การหาปริมาณต่างๆ
ที่เกี่ยวข้องกับการเคลื่อนที่แบบซิมเปิ้ลฮาร์มอนิก เช่น การกระจัด ความเร็ว
และความเร่งของนุภาค ณ ตำแหน่งต่างๆ เมื่อเวลาผ่านไป t ทั้งในแนวระดับและในแนวดิ่ง
สามารถหาได้โดยใช้ความรู้เกี่ยวกับการเคลื่อนที่ในแนววงกลม
เมื่อเวลาผ่านไป t ให้อนุภาคเคลื่อนที่ในแนวเฉพาะส่วนโค้งของวงกลมจากตำแหน่ง
A ไปอยู่ตำแหน่ง B ทำมุมที่จุดศูนย์กลาง ซึ่งเท่ากับ
ซึ่งเท่ากับ ดังรูป
ดังรูป
การหาการกระจัดในแนวระดับและในแนวดิ่ง
จากรูป พิจารณาในแนวระดับ จะได้
พิจารณาในแนวดิ่ง จะได้
พิจารณาความเร็วของเงาของอนุภาค
จากรูป ณ ตำแหน่ง B มีขนาด v
ซึ่งเท่ากับซึ่งเท่ากับ
 หรือ
หรือ  สามารถหาขนาดของความเร็วของเงาอนุภาคในแนวระดับและแนวดิ่งได้ ดังนี้
สามารถหาขนาดของความเร็วของเงาอนุภาคในแนวระดับและแนวดิ่งได้ ดังนี้
การหา  และ
และ 
XXXXXจากรูปXXXXXX และ
และ 

XXXXXXXXXXXXXXX

XXXXXและXXXXXXX

XXXXXXXXXXXXXX

XXXXXจากXXXXXXX

XXXXXXXXXXXXXX

XXXXXแทนค่า
 ในสมการ
ในสมการXXXXXได้ว่าXXXXX

XXXXXXXXXXXX

XXXXXและXXXXX

XXXXXXXXXXXX

XXXXXเครื่องหมาย
 หมายความว่า ณ ตำแหน่งหนึ่งๆ อนุภาคมีการเคลื่อนที่ไปและกลับ
หมายความว่า ณ ตำแหน่งหนึ่งๆ อนุภาคมีการเคลื่อนที่ไปและกลับXXXXXพิจารณาความเร่งของเงาของอนุภาค จากรูป ณ ตำแหน่ง B มีความเร่ง a ซึ่งเท่ากับ
 หรือ
หรือ  สามารถหาขนาดของความเร่งของเงาของอนุภาคในแนวระดับและแนวดิ่งๆ ได้ ดังนี้
สามารถหาขนาดของความเร่งของเงาของอนุภาคในแนวระดับและแนวดิ่งๆ ได้ ดังนี้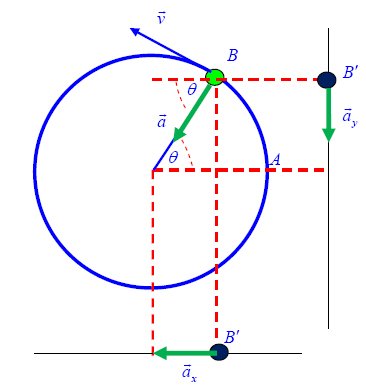
 และ
และ 
XXXXXจากรูปXXXXX

XXXXXหรือXXXXXX

XXXXXและXXXXXX

XXXXXXXXXXXXX

XXXXXหรือ XXXXX

XXXXXจากสมการที่ได้ออกมาเครื่องหมายมีค่าติดลบ (-) หมายความว่า ณ ตำแหน่ง B ความเร่ง a มีทิศตรงข้ามกับการกระจัด
 และ
และ 
การหาอัตราเร็วสูงสุด (
 ) และอัตราความเร่ง (
) และอัตราความเร่ง ( )
)XXXXXจากXXXXX

XXXXXณ ตำแหน่งสมดุล
 มีค่ามากที่สุด
มีค่ามากที่สุดXXXXXได้ว่าXXXXX

XXXXXดังนั้นXXXXX

XXXXXจากXXXXXXXXX

XXXXXณ ตำแหน่งไกลสุด y มากสุดเท่ากับ A a มีค่ามากที่สุด
XXXXXได้ว่าXXXXX

ถ้านำดินน้ำมันก้อนโตพอเหมาะติดไว้ที่ขอบวงล้อกลมหรือแผ่นไม้วงกลมซึ่งหมุนได้คล่องในแนวระดับ เมื่อหมุนวงล้อให้อัตราเร็วเชิงมุมสม่ำเสมอ ดินน้ำมันจะเคลื่อนที่ในแนววงกลมด้วยอัตราเร็วสม่ำเสมอด้วย เมื่อฉายลำแสงขนานในแนวระดับไปที่ดินน้ำมัน ดังรูป เงาของดินน้ำมันจะปรากฏบนฉากข้างหลัง โดยการเคลื่อนที่ของเงาจะกลับไปกลับมาในแนวตรงเป็นแบบฮาร์มอนิกอย่างง่าย
การฉายแสงผ่านวัตถุที่เคลื่อนที่เป็นวงกลม ปรากฏเงาบนฉากเป็น SHM
พิจารณาการเคลื่อนที่แบบวงกลมสัมพันธ์กับการเคลื่อนที่แบบซิมเปิลฮาร์โมนิค (S.H.M)
จากภาพจะเห็นว่าเมื่อวัตถุสีเหลืองเคลื่อนที่เป็นวงกลม เงาของวัตถุบนฉากจะเคลื่อนที่เป็นเส้นตรงกลับไป
กลับมา เรียกการเคลื่อนที่แบบซ้ำรอยเดิมนี้ว่า การเคลื่อนที่แบบซิมเปิลฮาร์โมนิค (Simple Harmonic Motion)
หรือการเคลื่อนที่แบบ S.H.M
เงาบนฉากของวัตถุที่เคลื่อนที่เป็นวงกลม ก็เหมือนกบการคิดองค์ประกอบทาง x ของการเคลื่อนที่ของจุดๆ หนึ่งเป็นวงกลมบนระนาบ xy ดังรูป 4.27 ให้ที่ขณะหนึ่งจุดนั้นอยู่ที่ตำแหน่งมุม
 หลังจากเคลื่อนที่มาแล้วเป็นเวลา t จากจุดตั้งต้นบนแกน x ดังรูป การเคลื่อนที่เป็นวงกลมที่มีอัตราเร็วสม่ำเสมอ ดังนั้น
หลังจากเคลื่อนที่มาแล้วเป็นเวลา t จากจุดตั้งต้นบนแกน x ดังรูป การเคลื่อนที่เป็นวงกลมที่มีอัตราเร็วสม่ำเสมอ ดังนั้น  ถ้าวงกลมมีรัศมี r จะมีองค์ประกอบของตำแหน่งบนแกน x คือ
ถ้าวงกลมมีรัศมี r จะมีองค์ประกอบของตำแหน่งบนแกน x คือ (4.16)
(4.16)และองค์ประกอบของความเร็วบนแกน x คือ
 (4.17)
(4.17)
จุด P เคลื่อนที่เป็นวงกลมอย่างสม่ำเสมอบนระนาบ xy
จากความเร่งในทิศเข้าหาจุดศูนย์กลางมีขนาดเท่ากับ
 หรือ
หรือ  จะได้องค์ประกอบของความเร่งบนแกน x คือ
จะได้องค์ประกอบของความเร่งบนแกน x คือ (4.18)
(4.18)จะเห็นว่าตำแหน่งทาง x ในสมการ (4.16) เป็นอย่างเดียวกับสมการ (4.14) เมื่อ เมื่อ เมื่อ เมื่อ
 ซึ่งเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย และเมื่อนำมาใช้ในสมการ (4.18) จะทำให้ได้ว่า
ซึ่งเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย และเมื่อนำมาใช้ในสมการ (4.18) จะทำให้ได้ว่า (4.19)
(4.19)สมการ (4.19) แสดงลักษณะสำคัญประการหนึ่งของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย นั่นคือ การมีความเร่งเป็นปฎิภาคกับการกระจัดแต่มีทิศตรงกันข้าม เนื่องจาก
 มีค่าคงตัว ทั้งนี้ทิศของความเร่งจะเป็นทิศเดียวกับแรง และแรงจะต้องเป็นแรงเข้าหาจุดสมดุลในขณะที่การกระจัดมีทิศออกไปจากสมดุล
มีค่าคงตัว ทั้งนี้ทิศของความเร่งจะเป็นทิศเดียวกับแรง และแรงจะต้องเป็นแรงเข้าหาจุดสมดุลในขณะที่การกระจัดมีทิศออกไปจากสมดุลสำหรับการเคลื่อนที่ของดินน้ำมันไปตามแนววงกลม เมื่อเคลื่อนที่ครบ 1 รอบใช้เวลาที่เรียกว่าหนึ่งคาบ (period) หรือ T หนึ่งรอบหมายถึงดินน้ำมันจะเคลื่อนที่ไป
 เรเดียน ดังนั้นอัตราเร็วเชิงมุม
เรเดียน ดังนั้นอัตราเร็วเชิงมุม  ของการเคลื่อนที่เป็นวงกลมจึงมีค่าเท่ากับ
ของการเคลื่อนที่เป็นวงกลมจึงมีค่าเท่ากับ  ส่วนเงาของดินน้ำมันที่เคลื่อนที่กลับไปกลับมารอบตำแหน่งสมดุลจะมีความถี่ของการเคลื่อนที่เป็น
ส่วนเงาของดินน้ำมันที่เคลื่อนที่กลับไปกลับมารอบตำแหน่งสมดุลจะมีความถี่ของการเคลื่อนที่เป็น  มีหน่วยเป็นรอบต่อวินาทีหรือเฮิรตซ์ (hertz, Hz) ความถี่เชิงมุม (
มีหน่วยเป็นรอบต่อวินาทีหรือเฮิรตซ์ (hertz, Hz) ความถี่เชิงมุม ( ) ของการเคลื่อนที่แบบ SHM มีค่าเป็น
) ของการเคลื่อนที่แบบ SHM มีค่าเป็น  ซึ่งมีค่าเหมือนกับอัตราเร็วเชิงมุม
ซึ่งมีค่าเหมือนกับอัตราเร็วเชิงมุม  และมีหน่วยเป็นเรเดียนต่อวินาทีเช่นเดียวกัน
และมีหน่วยเป็นเรเดียนต่อวินาทีเช่นเดียวกัน
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายของรถติดสปริง
เมื่อดึงรถทดลองให้สปริงยึดและรถออกจากตำแหน่งสมดุลเป็นระยะ A จะได้การกระจัดของรถทดลองมีค่า A และมีแรง
 ของสปริงดึงรถทดลองไปทางซ้าย ดัง รูป 4.28 ก. แรงนี้เรียกว่า แรงดึงกลับ (restoring force) มีค่าตาม
ของสปริงดึงรถทดลองไปทางซ้าย ดัง รูป 4.28 ก. แรงนี้เรียกว่า แรงดึงกลับ (restoring force) มีค่าตาม  ซึ่งแสดงว่าขนาดและแรงดึงกลับแปรผันตรงกับระระยืดหรือหดของสปริงหรือขนาดการกระจัด แต่แรงดึงกลับ
ซึ่งแสดงว่าขนาดและแรงดึงกลับแปรผันตรงกับระระยืดหรือหดของสปริงหรือขนาดการกระจัด แต่แรงดึงกลับ  มีทิศตรงข้ามกับการกระจัด
มีทิศตรงข้ามกับการกระจัด โดย k เป็นค่าคงตัวของสปริง
โดย k เป็นค่าคงตัวของสปริงเมื่อปล่อยมือ แรง
 จะดึงรถทดลองเคลื่อนที่กลับไปทางซ้ายเข้าหาตำแหน่งสมดุลด้วยความเร่ง
จะดึงรถทดลองเคลื่อนที่กลับไปทางซ้ายเข้าหาตำแหน่งสมดุลด้วยความเร่ง ทำให้ความเร็วมีขนาดเพิ่มขึ้นและมีทิศไปทางซ้าย ขนาดของแรง
ทำให้ความเร็วมีขนาดเพิ่มขึ้นและมีทิศไปทางซ้าย ขนาดของแรง จะลดลง เพราะขนาดการกระจัด
จะลดลง เพราะขนาดการกระจัด  ลดลง การเคลื่อนที่เป็นแบบฮาร์มอนิกอย่างง่าย เมื่อรถทดลองเคลื่อนที่ถึงตำแหน่งสมดุล ขนาดของการกระจัด
ลดลง การเคลื่อนที่เป็นแบบฮาร์มอนิกอย่างง่าย เมื่อรถทดลองเคลื่อนที่ถึงตำแหน่งสมดุล ขนาดของการกระจัด  เป็นศูนย์ ขนาดของ
เป็นศูนย์ ขนาดของ และ
และ ก็เป็นศูนย์แต่ความเร็ว
ก็เป็นศูนย์แต่ความเร็ว ของรถทดลองจะมีค่ามากที่สุดและมีทิศไปทางซ้าย ดังรูป 4.28 ค
ของรถทดลองจะมีค่ามากที่สุดและมีทิศไปทางซ้าย ดังรูป 4.28 คจากนั้นรถทดลองจะเคลื่อนที่ออกจากตำแหน่งสมดุลไปทางซ้ายต่อไปอีก และอัดลวดสปริงให้หดสั้น ลวดสปริงก็จะออกแรง
 มีทิศไปทางขวาต้านการเคลื่อนที่ของรถทดลอง ในขณะนี้รถทดลองจะเคลื่อนที่ด้วยความเร่ง
มีทิศไปทางขวาต้านการเคลื่อนที่ของรถทดลอง ในขณะนี้รถทดลองจะเคลื่อนที่ด้วยความเร่ง  ที่มีทิศไปทางขวาทำให้ความเร็วรถทดลองลดลงเรื่อยๆ จนกระทั่งความเร็วเป็นศูนย์ ขณะนี้รถทดลองมีการกระจัดค่า - A ดังรูป จ แล้วเคลื่อนที่ต่อไปดังรูปซึ่งเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย เราอาจเขียนกราฟของการกระจัดกับเวลาของการเคลื่อนที่ของรถทดลองในรูป ได้ดังรูป
ที่มีทิศไปทางขวาทำให้ความเร็วรถทดลองลดลงเรื่อยๆ จนกระทั่งความเร็วเป็นศูนย์ ขณะนี้รถทดลองมีการกระจัดค่า - A ดังรูป จ แล้วเคลื่อนที่ต่อไปดังรูปซึ่งเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย เราอาจเขียนกราฟของการกระจัดกับเวลาของการเคลื่อนที่ของรถทดลองในรูป ได้ดังรูป (3).jpg)
กราฟของการกระจัดของเวลาสำหรับหนึ่งรอบของการเคลื่อนที่
เมื่อพิจารณาการเคลื่อนที่ของรถทดลองติดปลายสปริงที่เคลื่อนที่ แรงที่สปริงกระทำต่อรถทดลองจะมีค่าเป็น F = - kx ถ้าให้ m เป็นมวลของรถทดลอง และ a เป็นความเร่งของรถทดลอง จากกฎการเคลื่อนที่ข้อที่ 2 ของนิวตัน
จะได้ F = ma = - kx
และ
 (4.20)
(4.20)นั่นคือ การเคลื่อนที่ของรถทดลองติดสปริงเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่าง่ายเช่นเดียวกับการเคลื่อนที่ของเงาของดินน้ำมัน มีความเร่งแปรผันตรงกับการกระจัด แต่มีทิศตรงกับข้าม
เทียบสมการ ( 4.20) กับสมการ (4.19) จะเห็นว่า ความเร่งคือ

ดังนั้น

 (4.21)
(4.21)ความถี่เชิงมุมของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย มีความสัมพันธ์กับค่าคงตัวของสปริง และมวลของวัตถุที่ติดกับสปริง ดังสมการ 4.21
การแกว่งของลูกตุ้มอย่างง่าย
ลูกตุ้มอย่างง่ายคือ ลูกตุ้มที่ประกอบด้วยมวลขนาดเล็ก ตามอุดมคติเป็นจุด แขวนที่ปลายด้ายหรือเชือกอ่อน โดยธรรมชาติวัตถุแขวนห้อยในแนวดิ่งเป็นตำแหน่งสมดุล เมื่อดึงวัตถุให้เอียงทำมุมเล็กๆ กับแนวดิ่งแล้วปล่อยให้วัตถุเคลื่อนที่แกว่งกลับไปมา ซึ่งจะพิสูจน์ได้ว่าเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
ลูกตุ้มอย่างง่ายคือ ลูกตุ้มที่ประกอบด้วยมวลขนาดเล็ก ตามอุดมคติเป็นจุด แขวนที่ปลายด้ายหรือเชือกอ่อน โดยธรรมชาติวัตถุแขวนห้อยในแนวดิ่งเป็นตำแหน่งสมดุล เมื่อดึงวัตถุให้เอียงทำมุมเล็กๆ กับแนวดิ่งแล้วปล่อยให้วัตถุเคลื่อนที่แกว่งกลับไปมา ซึ่งจะพิสูจน์ได้ว่าเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
ขณะเส้นเชือกเอียงทำมุมกับแนวดิ่งมีแรงกระทำเข้าหาจุดสมดุล
พิจารณาลูกตุ้มที่ผูกติดกับเชือกเบา
แล้วแกว่งไปมาในแนวดิ่งในทำนองเดียวกับการแกว่งของลูกตุ้มนาฬิกา โดยกำหนดให้
m เป็นมวลของลูกตุ้ม
L เป็นความยาวของเส้นเชือก
Q เป็นมุมที่เส้นเชือกทำกับแนวดิ่ง
จาก กับแนว
กับแนว เป็น
เป็น ดัง
ดัง ก็
ก็ อยู่
อยู่ ซึ่ง
ซึ่ง นี่
นี่
นั่น
ใน
ดัง มี
มี
ดัง
ระยะ= x = LQ
นั่น น้อย ๆ จึง
น้อย ๆ จึง
พิจารณา
จาก น้อย ๆ จะ
น้อย ๆ จะ
ดัง F = mg
จาก
ดัง
เนื่อง
ดัง a =  2x
2x
นั่นคือ  2x = g
2x = g
หรือ  2 =
2 = 
โดย w เป็นความถี่เชิงมุม (angular frequency) = 2 f
f
ดังนั้น  = 2
= 2 f =
f = 
 เอียงเป็นมุม
เอียงเป็นมุม  เรเดียนกับแนวดิ่ง
เรเดียนกับแนวดิ่ง
ลูกตุ้มมวล m จะมีแรงสองแรงกระทำต่อมวล m คือ น้ำหนักของลูกตุ้ม mg และแรงดึงในเส้นเชือก T ซึ่งทำมุม เรเดียนกับแนวดิ่ง ดังรูป สองแรงนี้รวมกันได้แรงลัพธ์เป็น
เรเดียนกับแนวดิ่ง ดังรูป สองแรงนี้รวมกันได้แรงลัพธ์เป็น  ตามแนวเส้นสัมผัสซึ่งตั้งฉากกับเส้นเชือก
ตามแนวเส้นสัมผัสซึ่งตั้งฉากกับเส้นเชือก
เนื่องจากแรง mg สามารถคิดแยกออกเป็น 2 แรงในแนวตั้งฉากกัน ดังรูป จะเห็นว่าแรง เป็นแรงที่ดึงมวล m กลับสู่ตำแหน่งสมดุล ให้แรงนี้เป็นแรง F ขณะที่
เป็นแรงที่ดึงมวล m กลับสู่ตำแหน่งสมดุล ให้แรงนี้เป็นแรง F ขณะที่  มีขนาดเท่ากับ T ทำให้เชือกตึงยาวเท่าเดิม เมื่อคำนึงถึงทิศด้วย แรงลัพธ์ F คือ
มีขนาดเท่ากับ T ทำให้เชือกตึงยาวเท่าเดิม เมื่อคำนึงถึงทิศด้วย แรงลัพธ์ F คือ

ถ้ามุม เป็นมุมเล็กๆ การเคลื่อนที่โค้งประมาณได้ว่าเป็นเส้นตรง คือการกระจัด x และ
เป็นมุมเล็กๆ การเคลื่อนที่โค้งประมาณได้ว่าเป็นเส้นตรง คือการกระจัด x และ  จะได้
จะได้
จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน F = ma
จะได้

จะเห็นว่า ความเร่งของลูกตุ้มแปรผันตรงกับการกระจัด และมีทิศตรงกันข้ามการแกว่งของลูกตุ้มจึงเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายด้วย
เนื่องจากอัตราเร่งของการแกว่ง
ดังนั้น
จาก จะได้
จะได้  (4.22)
(4.22)
หรือ (4.23)
(4.23)
สมการ (4.23) อาจนับว่าเป็นสมการที่ทำนายคาบของลูกตุ้มอย่างง่ายจากที่ได้วิเคราะห์มาตามหลักการของการเคลื่อนที่ที่ต้องเป็นไปตามกฎของนิวตัน
 เรเดียนกับแนวดิ่ง ดังรูป สองแรงนี้รวมกันได้แรงลัพธ์เป็น
เรเดียนกับแนวดิ่ง ดังรูป สองแรงนี้รวมกันได้แรงลัพธ์เป็น  ตามแนวเส้นสัมผัสซึ่งตั้งฉากกับเส้นเชือก
ตามแนวเส้นสัมผัสซึ่งตั้งฉากกับเส้นเชือกเนื่องจากแรง mg สามารถคิดแยกออกเป็น 2 แรงในแนวตั้งฉากกัน ดังรูป จะเห็นว่าแรง
 เป็นแรงที่ดึงมวล m กลับสู่ตำแหน่งสมดุล ให้แรงนี้เป็นแรง F ขณะที่
เป็นแรงที่ดึงมวล m กลับสู่ตำแหน่งสมดุล ให้แรงนี้เป็นแรง F ขณะที่  มีขนาดเท่ากับ T ทำให้เชือกตึงยาวเท่าเดิม เมื่อคำนึงถึงทิศด้วย แรงลัพธ์ F คือ
มีขนาดเท่ากับ T ทำให้เชือกตึงยาวเท่าเดิม เมื่อคำนึงถึงทิศด้วย แรงลัพธ์ F คือ
ถ้ามุม
 เป็นมุมเล็กๆ การเคลื่อนที่โค้งประมาณได้ว่าเป็นเส้นตรง คือการกระจัด x และ
เป็นมุมเล็กๆ การเคลื่อนที่โค้งประมาณได้ว่าเป็นเส้นตรง คือการกระจัด x และ  จะได้
จะได้จากกฎการเคลื่อนที่ข้อที่สองของนิวตัน F = ma
จะได้


จะเห็นว่า ความเร่งของลูกตุ้มแปรผันตรงกับการกระจัด และมีทิศตรงกันข้ามการแกว่งของลูกตุ้มจึงเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่ายด้วย
เนื่องจากอัตราเร่งของการแกว่ง

ดังนั้น

จาก
 จะได้
จะได้  (4.22)
(4.22)หรือ
 (4.23)
(4.23)สมการ (4.23) อาจนับว่าเป็นสมการที่ทำนายคาบของลูกตุ้มอย่างง่ายจากที่ได้วิเคราะห์มาตามหลักการของการเคลื่อนที่ที่ต้องเป็นไปตามกฎของนิวตัน
โจทย์การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
วิดีโอแสดงการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
แหล่งที่มาที่ใช่ประกอบบทความ
http://www.school.net.th/library/snet3/supinya/harmonic-pen/pendulum.htm














(2).jpg)








