การเคลื่อนที่แบบต่างๆ: Ferris wheel Motion

การเคลื่อนที่แบบวงกลม(Circular Motion)

การเคลื่อนที่แบบวงกลมหรือส่วนของวงกลม

การเคลื่อนที่แบบวงกลมเป็นการเคลื่อนที่อีกแบบหนึ่งที่น่าสนใจ เพราะการเคลื่อนที่หลายอย่างรอบตัวเรา มีส่วนที่จะเป็นการเคลื่อนที่เป็นวงกลม ตัวอย่างเช่น การเคลื่อนที่ดังรูป รถยนต์หรือรถจักรยานยนต์กำลังเลี้ยวโค้ง รถไฟตีลังกา หรือดาวเทียมโคจรรอบโลก นับเป็นการเคลื่อนที่แบบวงกลมหรือส่วนของวงกลม รถยนต์ รถจักรยานยนต์ และ ดาวเทียม เคลื่อนที่ในแนววงกลมหรือส่วนของวงกลม ได้อย่างไร หรือทำไมการเคลื่อนที่เป็นแบบนั้นๆ ได้ จะศึกษาต่อไป

เพื่อความเข้าใจการเคลื่อนที่เป็นวงกลม เราควรเริ่มศึกษาจากการเคลื่อนที่เป็นวงกลมที่มีอัตราเร็วคงตัวก่อน นั่นคือการเคลื่อนที่ที่มีขนาดของความเร็วเท่าเดิม สม่ำเสมอแต่มีทิศเปลี่ยนไปทีละน้อย

การแกว่งวัตถุให้เคลื่อนที่เป็นวงกลมในระนาบระดับ

เราอาจหาประสบการณ์จากการแกว่งวัตถุที่ปลายเชือกให้เป็นวงกลมในระนาบระดับดังรูป ในการแกว่งที่รัศมีค่าหนึ่ง เราจะรู้สึกว่า มือจะต้องใช้แรงดึงมากขึ้นเมื่อแกว่งให้เร็วขึ้น (เวลาครบรอบสั้นลง) แสดงว่าการทำให้วัตถุเคลื่อนที่เป็นวงกลมจะต้องใช้แรงดึง การแสดงว่า การเคลื่อนที่เป็นวงกลมหรือการเคลื่อนที่เป็นแนวโค้งของวัตถุต้องใช้แรงก็คือ การใช้อุปกรณ์สาธิตที่ดีดลูกกลมโลหะให้เคลื่อนที่ไปตามรางโค้งวงกลม ดังรูปจะสังเกตได้ว่าเมื่อสุดรางโค้ง ลูกโลหะจะวิ่งตรงต่อไป แสดงว่าวัตถุวิ่งโค้งได้เนื่องจากมีรางบังคับ และจะต้องมีแรงจากรางกระทำอยู่ตลอดเวลา แรงดังกล่าวเป็นแรงกระทำจากขอบรางซึ่งเกิดขึ้นเนื่องจากลูกกลมโลหะเคลื่อนที่สัมผัสกับราง ณ ตำแหน่งต่างๆ ในทิศตั้งฉากกับราง จึงมีทิศเข้าหาศูนย์กลางของการเคลื่อนที่ดังรูป

รูป ลูกกลมโลหะเคลื่อนที่ไปตามรางโลหะที่เป็นส่วนโค้งวงกลม

รูป แรงกระทำกับลูกกลมโลหะขณะเคลื่อนที่ไปตารางโค้ง

การเคลื่อนที่แบบวงกลมมีความเร่งสู่ศูนย์กลาง

เราอาจพิสูจน์ได้ว่าวัตถุเคลื่อนที่เป็นวงกลมมีความเร่ง จากความหมายของความเร่ง คือ อัตราการเปลี่ยนความเร็ว การเคลื่อนที่เป็นวงกลมที่มีขนาดของความเร็วคงตัว แต่มีการเปลี่ยนทิศของความเร็วตลอดเวลา ซึ่งจะถือว่ามีการเปลี่ยนความเร็ว และมีความเร่งดังต่อไปนี้

พิจารณาการเคลื่อนที่ของวัตถุในแนววงกลมรัศมี r ด้วยขนาดความเร็วคงตัว v จากตำแหน่ง A ไปยังตำแหน่ง B โดยผ่านตำแหน่ง C ที่อยู่บนแกน y ดังรูป 4.14 ถ้าให้ A และ B อยู่ห่างจากแกน y เท่ากัน และที่ตำแหน่ง A กับ B วัตถุมีความเร็ว $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _A$ และ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _B$ ตามลำดับ

รูป การเปลี่ยนแปลงความเร็วของวัตถุซึ่งเคลื่อนที่ในแบบวงกลม

เมื่อพิจารณาแต่ขนาดของ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _A$ และ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _B$ จะได้ v_A = v_B = v

และจะได้ว่า
                    ความเร็วองค์ประกอบของ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _A$ ในแนวแกน   x    =    $+ v_A \cos \theta$
                    ความเร็วองค์ประกอบของ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _A$ ในแนวแกน   y    =    $+ v_A \sin \theta$
                    ความเร็วองค์ประกอบของ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _B$ ในแนวแกน   x    =    $+ v_B \cos \theta$
                    ความเร็วองค์ประกอบของ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over v} _B$ ในแนวแกน   y    =    $- v_B \sin \theta$
                    เมื่อ   $\theta$ เป็นมุมระหว่างเส้นรัศมีมีที่ตำแหน่ง A กับ C หรือมุมระหว่างเส้นรัศมีที่ตำแหน่ง B กับ C พิจารณาช่วงเวลาที่วัตถุใช้ในการเคลื่อนที่จาก A ไป B ด้วยอัตราความเร็วคงตัว v จะได้

   $t = \frac{{ÊèÇ¹â¤é§ AB}}{v}$
                    จากรูปเราสามารถหา ความยาวของส่วนโค้ง AB ได้เป็น $(2\theta )r$ ดังนั้น

สำหรับการเคลื่อนที่ของวัตถุบนส่วนโค้ง AB ความเร็วในแกน X ที่ A และที่ B จะมีค่าเท่ากันคือ

$v_A \cos \theta = v_B \cos \theta = v\cos \theta$ ดังนั้นความเร่งในแนวแกน X จึงเท่ากับศูนย์ และ
เราสามารถหาความเร่งเฉลี่ยตามแนวแกน y คือ a_y

ได้จาก   $a = \frac{{v - u}}{t}$
                    แทนค่า                      $a_y = ( - v_B \sin \theta - v_A \sin \theta )\frac{v}{{2\theta r}}$
                                                      $a_y = - \frac{{v^2 }}{r}\left( {\frac{{\sin \theta }}{\theta }} \right)$
เครื่องหมาย - แสดงว่า ความเร่ง   a_y

มีทิศทางไป - y คือตำแหน่ง C เข้าหาจุด ศูนย์กลาง O
เมื่อให้มุม $\theta$ มีค่าน้อยจนเกือบเป็นศูนย์ เพื่อให้ A และ B เข้าใกล้ตำแหน่ง C ซึ่งอยู่ตรงส่วนบนสุดของวงกลม ดังนั้นความเร่ง a_y

ก็จะเป็นความเร่งขณะหนึ่งคือความเร่งที่ตำแหน่ง C มีทิศเข้าหาจุดศูนย์กลาง O ของวงกลม การหาขนาดของความเร่งขณะหนึ่งจะพิจารณาว่า   $\sin \theta = \theta$ เพราะ $\theta$ มีค่าน้อยเข้าใกล้ศูนย์ และ
จะได้   $a_y = \frac{{v^2 }}{r}$ ซึ่งมีทิศเข้าสู่จุดศูนย์กลางของวงกลม

     ในทำนองเดียวกัน ถ้าย้ายตำแหน่ง C มาอยู่บนแนวแกน X แทน โดยให้ A และ B อยู่ห่างจาก C เท่ากันเช่นเดิม ก็จะได้ว่าความเร่งขณะหนึ่งที่ตำแหน่ง C จะมีทิศในแนวแกน X และเข้าหาจุดศูนย์กลางเช่นเดิม และไม่ว่าจะย้าย C ไปอยู่ที่ตำแหน่งใดบนเส้นรอบวงกลม ก็จะได้ว่าความเร่งขณะหนึ่งที่ตำแหน่ง C มีทิศเข้าหาจุดศูนย์กลางเสมอ
ดังนั้นถ้าให้   a_c

เป็นความเร่งขณะหนึ่งที่มีทิศเข้าสู่ศูนย์กลางวงกลม
จะได้ $a_c = \frac{{v^2 }}{r}$ (4.4)
เมื่อวัตถุมีความเร่งทิศเข้าสู่ศูนย์กลาง ดังนั้นวัตถุเคลื่อนที่ในแนววงกลมด้วยอัตราเร็วคงตัว ต้องมีแรงสู่ศูนย์กลางกระทำต่อวัตถุตามกฎของนิวตัน แรงสู่ศูนย์กลาง F_c

จะเป็น
$F_c = ma_2 \frac{{mv^2 }}{r}$ (4.5)

เราสามารถทำการทดลองเพื่อสำรวจว่า การเคลื่อนที่แบบวงกลมมีแรงสู่ศูนย์กลางหรือไม่ หรือเพื่อพิสูจน์ว่าแรงสู่ศูนย์กลางเป็นไปตามสมการ (4.5) หรือไม่ ดังรายละเอียดท้ายเรื่อง $t = \frac{{2\theta r}}{v}$

การเคลื่อนที่บนโค้ง
       ในกรณีของรถยนต์ที่กำลังเลี้ยวโค้ง แรงเสียดทานที่พื้นถนนกระทำกับด้านข้างของยางรถจะเป็นแรงสู่ศูนย์กลางที่ทำให้รถยนต์เลี้ยวโค้งได้ และเนื่องจากแรงเสียดทานมีค่าจำกัดขึ้นกับสภาพถนนและยางรถ ดังนั้นแรงสู่ศูนย์กลางที่เป็นไปได้จึงมีค่าจำกัดด้วย ถ้าถนนมีรัศมีความโค้งขนาดหนึ่ง อัตราเร็วที่รถวิ่งขณะเลี้ยวโค้งจะต้องไม่มากเกินกว่าที่ถนนจะสามารถให้แรงเสียดทานทิศสู่ศูนย์กลางที่เป็นไปตามสมการ (4.4) ได้ หากอัตราเร็วเกินรถจะไถลออกนอกโค้ง ดังที่เกิดขึ้นเป็นอุบัติเหตุที่เป็นข่าวบ่อยครั้ง โดยเฉพาะเมื่อฝนตก ถนนลื่นแรงเสียดทานที่เป็นไปได้จะลดลง

ตัวอย่าง 1 รถยนต์มวล 1,000 กิโลกรัม แล่นด้วยความเร็ว 60 กิโลเมตรต่อชั่วโมงเลี้ยวโค้งบนถนน ที่มีผิวอยู่ในแนวระดับและมีทางโค้ง 2 โค้ง ซึ่งมีรัศมีความโค้ง 100 เมตร และ 500 เมตร ตามลำดับ
      1.    แรงสู่ศูนย์กลางที่กระทำต่อรถยนต์ในแต่ละกรณีมีค่าเท่าใด
      2.    ถ้าแรงเสียดทานที่พื้นถนนกระทำกับยางรถในทิศเข้าสู่ศูนย์กลางมีค่าสูงสุดเท่ากับ 1,000 นิวตัน จะมีผลอย่างไรต่อการเลี้ยวโค้งของรถยนต์ทั้งสองกรณี
      วิธีทำ
            1. กรณีที่ถนนระดับมีรัศมีความโค้ง 100 เมตร
                                 จาก            $F_c = \frac{{mv^2 }}{r}$
          ในที่นี้ m   =   1000 kg,    $v = \frac{{60 \times 10^3 }}{{3600}}m/s$ และ r = 100 m

แทนค่า                      $F_c = \frac{{1000kg}}{{100m}} \times \left( {\frac{{60 \times 10^3 }}{{3600}}m/s} \right)^2$
                             F_c

= 2,778 N
คำตอบ     แรงสู่ศูนย์กลางกระทำต่อรถยนต์ขณะเลี้ยวโค้งบนถนนระดับรัศมีความโค้ง 100 เมตร เท่ากับ 2,778 นิวตัน

        กรณีที่ถนนระดับมีรัศมีความโค้ง   500 เมตร

                       จาก   $F_c = \frac{{mv^2 }}{r}$
                      ในที่นี้ m     =     1000 kg   $v = \frac{{60 \times 10^3 }}{{3600}}m/s$ และ r = 500 m

แทนค่า                  $F_c = \frac{{1000kg}}{{500m}} \times \left( {\frac{{60 \times 10^3 }}{{3600}}m/s} \right)^2$
                                F_c

= 555.6 N

คำตอบ แรงสู่ศูนย์กลางกระทำต่อรถยนต์ขณะเลี้ยวโค้งบนถนนระดับรัศมีความโค้ง 500 เมตร เท่ากับ 555.6 นิวตัน

2. เนื่องจากแรงสู่ศูนย์กลางที่กระทำต่อรถยนต์มีค่าสูงสุด 1,000 นิวตัน รถยนต์จะต้องเลี้ยวโค้งด้วยแรงสู่ศูนย์กลางที่น้อยกว่าหรือเท่ากับแรงสู่ศูนย์กลางสูงสุดจึงจะเลี้ยวโค้งได้อย่างปลอดภัย

 คำตอบ กรณีที่รัศมีของทางโค้ง 100 เมตร ต้องใช้แรงสู่ศูนย์กลางถึง 2,778 นิวตัน ดังนั้นรถยนต์จึงไม่สามารถเลี้ยวโค้งได้ เป็นเหตุให้รถไถลออกนอกถนน แต่กรณีที่รัศมีของทางโค้ง 500 เมตรจะใช้แรงสู่ศูนย์กลางเพียง 555.6 นิวตัน ดังนั้นรถยนต์จึงสามารถเลี้ยวโค้งได้อย่างปลอดภัย
 จากตัวอย่าง 4.3 ทำให้วิเคราะห์ได้ว่ารถยนต์แล่นเลี้ยวโค้งบนถนนระดับที่มีรัศมีความโค้งไม่เท่ากันแต่ด้วยอัตราเร็วเท่ากัน จะมีแรงสู่ศูนย์กลางไม่เท่ากัน ทางโค้งที่มีรัศมีความโค้งสั้น รถยนต์จะใช้แรงสู่ศูนย์กลางมากกว่าทางโค้งที่มีรัศมีความโค้งยาว ดังนั้นรถยนต์ที่เลี้ยวโค้งที่มีรัศมีความโค้งน้อย ไม่ควรเลี้ยวด้วยอัตราเร็วเท่ากับการเลี้ยวโค้งบนทางที่มีรัศมีความโค้งมากกว่า เนื่องจากแรงเสียดทานที่ถนนกระทำกับรถซึ่งเป็นแรงสู่ศูนย์กลางมีค่าจำกัด อาจมีค่าไม่พอที่จะทำให้รถเลี้ยวโค้งได้อย่างปลอดภัย ผู้ขับขี่ยวดยานจึงต้องใช้ความเร็วตามที่กำหนดอย่างเคร่งครัด อย่างไรก็ตาม ถ้าต้องการให้รถเลี้ยวโค้งได้อย่างปลอดภัยด้วยอัตราเร็วที่มากขึ้น จำเป็นต้องหาแรงอื่นมาเสริมแรงเสียดทานเพื่อเพิ่มแรงสู่ศูนย์กลางขึ้นให้เหมาะสม

 การเลี้ยวโค้งบนถนนระดับของรถจักรยานยนต์หรือรถจักรยาน ขณะรถจักรยานยนต์หรือรถจักรยานแล่นในแนวตรงบนถนนระดับ ถ้าพิจารณาแรงทั้งหมดที่กระทำกับรถและคนนอกจากแรงเสียดทานที่กระทำที่ล้อรถทำให้รถเคลื่อนที่ไปข้างหน้าได้ ยังมีน้ำหนักของรถและคน $m\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over g}$ และแรงที่พื้นดันรถและคนในทิศตั้งฉาก $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}$ รถและคนจะต้องตั้งตรง แนวของ $m\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over g}$ และ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}$ จึงจะผ่านศูนย์กลางมวลรวมของรถและคนและอยู่ในแนวดิ่ง ทำให้ไม่มีโมเมนต์ของแรงที่จะทำให้รถล้ม รถจึงไม่ล้ม ดังรูป 4.15 ก.

รูป แสดงแรงกระทำต่อรถจักรยานยนต์

เมื่อรถจักรยานยนต์หรือรถจักรยานเลี้ยวโค้ง จะต้องมีแรงกระทำต่อรถเพิ่มอีก 1 แรง คือแรงเสียดทาน $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over f}$ ที่พื้นถนนกระทำกับด้านข้างของล้อรถในทิศเข้าหาจุดศูนย์กลางของความโค้งรถจำเป็นต้องเอียงตัว เพื่อให้ไม่มีโมเมนต์ของแรงที่จุดศูนย์กลางมวล ดังรูป 4.15 ข.ถ้าคนและรถไม่เอียงตัว แรงลัพธ์ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R}$ ของแรง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over f}$ และ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}$ จะไม่ผ่านศูนย์กลางมวล ดังรูป 4.15 คำให้มีโมเมนต์ของแรง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over R}$ (คิดรอบจุดศูนย์กลางมวล) เป็นเหตุให้มีการหมุนรอบจุดศูนย์กลางมวล และรถล้ม

การยกขอบของถนนโค้ง

แรงที่กระทำต่อรถขณะที่กำลังแล่นเลี้ยวโค้งบนถนเอียงทำมุมกับพื้นระดับ

เพื่อให้การเลี้ยวโค้งด้วยความเร็วเป็นไปได้ง่ายขึ้นและปลอดภัยขึ้น พื้นถนนโค้งจะถูกยกให้เอียงโดยให้ขอบถนนด้านนอกสูงกว่าขอบด้านใน เมื่อรถแล่นเลี้ยวโค้งบนพื้นถนนที่เอียงด้วยขนาดของความเร็วพอดีตามที่วิศวกรออกแบบไว้ ไม่ว่าจะเป็นรถยนต์ หรือรถจักรยานยนต์ แรงที่ถนนกระทำต่อรถจะพอดีและอยู่ในทิศตั้งฉากกับพื้นเอียงได้ ที่ความเร็วนั้นจึงไม่มีแรงเสียดทาน   $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over f}$ ที่พื้นถนนกระทำต่อด้านข้างของล้อรถ องค์ประกอบของแรงตั้งฉากกับถนนในทิศขนานกับพื้นระดับ $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}$ จะทำให้เกิดแรงสู่ศูนย์กลาง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over F} _c$ ดังรูป 4.17 โดยไม่ต้องอาศัยแรง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over f}$ ถ้ารถวิ่งด้วยอัตราเร็วที่ไม่พอดีรถจึงจะอาศัยแรง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over f}$ ช่วย องค์ประกอบของแรง $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over N}$ ในแนวระดับคือ $N\sin \theta$ เมื่อยกขอบถนนให้เอียงทำมุม $\theta$ กับแนวระดับและวิ่งด้วยอัตราเร็วพอดีจากรูป 4.16 แรงสู่ศูนย์กลางคือ $N\sin \theta$
                                                              จาก      $F_c = \frac{{mv^2 }}{r}$
                                                   ดังนั้น   $N\sin \theta = \frac{{mv^2 }}{r}$
                                                  และ      $N\cos \theta = mg$
                                                   ดังนั้น   $\frac{{N\sin \theta }}{{N\cos \theta }}= \frac{{mv^2 }}{{rmg}}$
                                                   หรือ       $\tan \theta = \frac{{v^2 }}{{rg}}$                                                          (4.6)
          สมการ 4.6 แสดงให้เห็นว่าในการสร้างถนนทางโค้งให้เอียงทำมุมกับแนวระดับนั้นต้องคำนึงถึงอัตราเร็วของรถขณะเลี้ยวและรัศมีของทางโค้งเพื่อให้การขับรถปลอดภัย

ตัวอย่าง 2        รถยนต์คันหนึ่งแล่นด้วยอัตราความเร็ว 60 กิโลเมตรต่อชั่วโมง บนถนนโค้งที่มีรัศมีความโค้ง 150 เมตร ถ้าไม่คิดแรงเสียดทาน พื้นถนนควรเอียงทำมุมเท่าไร กับแนวระดับรถจึงจะเลี้ยวได้อย่างปลอดภัย

                   วิธีทำ     การหามุมที่พื้นถนนทำกับแนวระดับ หาได้จากสมการ
                                                $\tan \theta = \frac{{v^2 }}{{rg}}$
                   ในที่นี้                  v = 16.67 m/s และ r = 150 m
                   แทนค่า    $\tan \theta = \frac{{(16.67m/s)^2 }}{{150m \times 9.8m/s^2 }} = 0.189$
                                    $\theta = 10.7^\circ$
                   คำตอบ พื้นถนนจะต้องเอียงทำมุม 10.7 องศากับแนวระดับรถจึงจะเลี้ยวได้อย่างปลอดภัย

ตัวอย่าง 3 รถยนต์มวล 1,550 กิโลกรัม แล่นเลี้ยวบนถนนระดับ ซึ่งมีรัศมีความโค้ง 50 เมตร ด้วยอัตราเร็ว 36 กิโลเมตรต่อชั่วโมง จงหาแรงเสียดทานระหว่างพื้นถนนกับยางรถที่มีค่าน้อยที่สุดที่ทำให้รถยนต์สามารถเลี้ยวได้อย่างปลอดภัย

                   วิธีทำ     แรงเสียดทานระหว่างพื้นถนนกับยางรถที่มีค่าน้อยที่สุดที่ทำให้รถยนต์สามารถเลี้ยวโค้งได้ คือแรงสู่ศูนย์กลาง
                                                  $F_c = \frac{{mv^2 }}{r}$
           จะได้แรงสู่ศูนย์กลาง    ในที่นี้             m   =   1,550 kg, v =   10   m/s   และ   r   =   50 m
                       แทนค่า               $F_c = \frac{{1550kg \times (10m/s)^2 }}{{50m}}$
                       จะได้แรงสู่ศูนย์กลาง [texF]_c[/tex] =   3,100 N
                คำตอบ แรงเสียดทานระหว่างพื้นถนนกับยางรถที่มีค่าน้อยที่สุดทำให้รถยนต์สามารถเลี้ยวได้อย่างปลอดภัย เท่ากับ 3,100 นิวตัน
          เราสามารถใช้ความรู้ที่ศึกษามานี้อธิบายการเคลื่อนที่แบบวงกลมในแนวระดับของวัตถุในลักษณะอื่นๆ ได้ เช่น เพนดูลัมกรวย ได้เช่นกัน

          ตัวอย่าง 4 ถ้าแกว่งเชือกยาว l ซึ่งเป็นวัตถุมวล m ผูกที่ปลายให้เคลื่อนที่แบบเพนดูลัมกรวย รัศมีของการเคลื่อนที่แบบวงกลมเท่ากับ r และวัตถุเคลื่อนที่ด้วยอัตราเร็วคงตัว v จงหามุม $\theta$ ที่เส้นเชือกทำกับแนวดิ่ง

แสดงแรงกระทำต่อวัตถุที่กำลังเคลื่อนที่แบบเพนดูลัม

วิธีทำ
ให้ T เป็นแรงดึงในเส้นเชือก แรงองค์ประกอบของ T ในแนวระดับเท่ากับ $T\sin \theta$ ซึ่งเป็นแรงสู่ศูนย์กลาง F_c

                จาก               $F_c = \frac{{mv^2 }}{r}$
                แทนค่า         $T\sin \theta = \frac{{mv^2 }}{r}$
                แรงองค์ประกอบของ T ในแนวดิ่งคือ   $T\cos \theta$ ซึ่งมีขนาดเท่ากับน้ำหนัก mg แต่กระทำต่อวัตถุในแนวตรงข้ามกัน ในสมดุล
                         $T\cos \theta = mg$
                จะได้      $\frac{{T\sin \theta }}{{T\cos \theta }} = \frac{{mv^2 }}{r}\frac{1}{{mg}}$
                          $\tan \theta = \frac{{v^2 }}{{rg}}$

          คำตอบ   มุมที่เส้นเชือกทำกับแนวดิ่งเท่ากับ $\tan ^{ - 1} = (\frac{{v^2 }}{{rg}})$

การเคลื่อนที่แบบวงกลมในระนาบดิ่ง
การเคลื่อนที่แบบวงกลมในระนาบดิ่ง ได้แก่ การเคลื่อนที่ของลูกกลมโลหะไปตามรางรูปวงกลมในระนาบดิ่ง ทุกๆ หนแห่งที่ลูกกลมโลหะเคลื่อนที่ผ่านจะมีแรงสู่ศูนย์กลางกระทำต่อลูกกลมโลหะเพื่อเปลี่ยนทิศของความเร็ว แรงสู่ศูนย์กลางมีค่าอย่างไรเมื่อลูกกลมโลหะอยู่ ณ ตำแหน่งต่างๆ ในรางรูปวงกลมจะต้องระลึกว่า เพราะลูกกลมถูกแรงโน้มถ่วงกระทำอยู่ตลอดเวลาด้วย ผลของแรงโน้มถ่วงที่กระทำนี้ จะทำให้อัตราเร็วของการเคลื่อนที่ไม่สามารถจะรักษาให้คงตัวได้ แต่จะต้องเป็นไปตามหลักการอนุรักษ์พลังงาน

รูป การเคลื่อนที่เป็นวงกลมในระนาบดิ่ง

การคิดหาค่าแรงที่ต้องการที่จะกระทำให้วัตถุวิ่งโค้ง อาจทำได้ตามหลักเกณฑ์ปกติ เช่น กรณีลูกกลมโลหะอยู่ ณ ตำแหน่งล่างสุดของรางวงกลม แรงที่รางกระทำกับวัตถุจะเป็นเท่าใด ขณะที่วัตถุมีอัตราเร็ว v และรางมีรัศมีความโค้งเป็น r

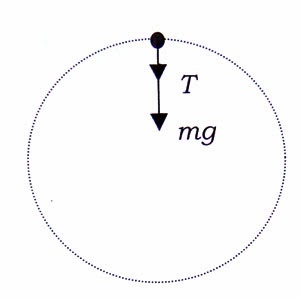
แรงต่อการเคลื่อนที่เป็นวงกลมในระนาบดิ่งที่จุดต่ำสุด

ถ้าให้

เป็นแรงสู่ศูนย์กลาง จะได้
                                               $\frac{{mv^2 }}{r} = F_c = N - mg$
                           แสดงว่า   แรงที่รางดันลูกกลมโลหะในทิศตั้งฉาก
                                       กับราง   $N = \frac{{mv^2 }}{r} + mg$
          แรงกระทำต่อวัตถุที่ตำแหน่งอื่นอาจจะหาได้ในทำนองเดียวกัน

ตัวอย่าง 5 ผูกวัตถุมวล 1 กิโลกรัม ด้วยเส้นเชือกยาว 1 เมตร แกว่งวัตถุให้เคลื่อนที่เป็นแนววงกลมในระนาบดิ่ง จงหาอัตราเร็ว ณ ตำแหน่งสูงสุด เมื่อแรงดึงในเส้นเชือกเท่ากับ 6 นิวตัน (กำหนดให้ g = 10 เมตร/วินาที

)

สำหรับตัวอย่าง

   วิธีทำ                             อัตราเร็ว ณ ตำแหน่งสูงสุดสามารถหาได้จาก
                                                $F_c = \frac{{mv^2 }}{R}$
                             ในที่นี้แรงสู่ศูนย์กลางมาจากแรงดึงและน้ำหนักดังนั้น
                                                F_c

= (1kg ) x (10 m/s

) +6N
= $\frac{{mv^2 }}{R}$
แทนค่ามวลและรัศมี จะได้ v^2

= 16 หรือ v = 4.0 m/s

คำตอบ อัตราเร็ว ณ ตำแหน่งสูงสุดเท่ากับ 4.0 เมตรต่อวินาที

อัตราเร็วเชิงมุม
การเคลื่อนที่ของวัตถุในแนววงกลมเป็นการเคลื่อนที่ในระนาบ xy ด้วยอัตราเร็วคงตัวระยะทางที่วัตถุเคลื่อนที่ไปได้ใน 1 หน่วยเวลาเป็นอัตราเร็วเชิงเส้น นอกจากวัตถุจะมีอัตราเร็วเชิงเส้นแล้วยังมีอัตราเร็วเชิงมุมซึ่งหมายถึง มุมที่รัศมีกวาดไปได้ใน 1 หน่วยเวลา ในรูป แสดงให้เห็นว่าเราใช้มุม $\theta$ ที่วัตถุกวาดไปบนเส้นรอบวงกลมบอกตำแหน่งของวัตถุได้ ซึ่ง $\theta = \frac{s}{r}$ โดย s เป็นระยะทางบนส่วนโค้งวงกลมที่วัตถุกวาดไป และ r เป็นรัศมีวงกลม มุม $\theta$ ที่กำหนดในลักษณะนี้จะวัดเป็นเรเดียนซึ่งเป็นค่าตัวเลขการเปรียบเทียบตำแหน่งบนเส้นรอบวงกลมจากแนวอ้างอิง (ในรูปนี้คือแนวแกน x)
เนื่องจากความยาวของเส้นรอบวงกลม 1 รอบคือ $2\pi r$ ดังนั้นมุมที่กวาดไปครบ 1 รอบจึงเป็น $2\pi$ เรเดียน

แสดงวัตถุเคลื่อนที่ในแนววงกลมจาก A ไป B

          จากรูป วัตถุเคลื่อนที่ในแนววงกลมรัศมี r ด้วยอัตราเร็วคงตัว v ถ้าวัตถุเคลื่อนที่จาก A ไป B ใช้เวลา t และรัศมีวงกลมกวาดไปเป็นมุม $\theta$ ค่ามุมที่กวาดไปได้ในเวลา 1 หน่วยเวลาเรียกว่า  อัตราเร็วเชิงมุม ใช้สัญลักษณ์ $\omega$ มีหน่วยเป็น เรเดียนต่อวินาที หรือ rad/s จะหาค่าได้จาก
                                         $\omega = \frac{\theta }{t}$ (4.7)

          ถ้าวัตถุเริ่มเคลื่อนที่จาก A ไปตามเส้นรอบวงกลมและกลับมาที่ A อีกครั้งหนึ่ง เป็นการเคลื่อนที่ครบ 1 รอบ จะได้เวลาในการเคลื่อนที่ครบ 1 รอบ คือ คาบ T   และมุมที่รัศมีกวาดไปครบ 1 รอบเป็น $2\pi$ เรเดียน
          ดังนั้น                    $\omega  = \frac{{2\pi }}{T}$                                                             (4.8)
และในการเคลื่อนที่ครบ 1 รอบ จะได้ระยะทาง $2\pi r$
          ดังนั้น อัตราเร็วเชิงเส้น     $v = \frac{{2\pi r}}{T}$ (4.9)
จะได้ความสัมพันธ์ระหว่าง v กับ $\omega$ เป็น
                                            $v = \omega r$
            จาก                           $a_c = \frac{{v^2 }}{r}$
           จะได้                          $a_c = \omega ^2 r$
        จาก  (4.10)                   F_c = ma_c

         จะได้(4.11)                  $F_c = m\omega ^2 r$
          สมการ (4.10) และ (4.11) เป็นการเขียนความเร่งและแรงสู่ศูนย์กลางในรูปของอัตราเร็วเชิงมุม

ตัวอย่าง 6 โลกหมุนรอบตัวเองครบ 1 รอบ ใช้เวลา 24 ชั่วโมง และรัศมีของโลกเท่ากับ 6.37 x 10⁶เมตร จงคำนวณหา
ก.อัตราเร็วเชิงมุมของวัตถุบนผิวโลก
ข.อัตราเร็วเชิงเส้นและขนาดของความเร่งสู่ศูนย์กลางของวัตถุที่อยู่บนเส้นศูนย์สูตรของโลก
วิธีทำ
          วัตถุบนโลกเคลื่อนที่ในแนววงกลมตลอดเวลา และเคลื่อนที่ครบ 1 รอบใช้เวลา 24 ชั่วโมง เนื่องจากโลกหมุนรอบตัวเอง
ก.    หาอัตราเร็วเชิงมุมของวัตถุ
                  จาก                         $\omega = \frac{{2\pi }}{T}$
              ในที่นี้                       T   =   86400 s
แทนค่า                                $\omega = \frac{{2 \times 3.0142}}{{86400}} = 7.27 \times 10^{ - 5} rad/s$

คำตอบ     อัตราเร็วเชิงมุมของวัตถุบนผิวโลกเท่ากับ $7.27 \times 10^{ - 5}$ เรเดียนต่อวินาที
ข.    หาอัตราเร็วเชิงเส้นของวัตถุที่อยู่บนเส้นศูนย์สูตร
จาก                        $v = \omega r$
ซึ่ง                          $\omega = 7.27 \times 10^{ - 5} rad/s$ และ r = 6.37x 10⁶ m
แทนค่า                      $v = (7.27 \times 10^{ - 5} rad/s) \times (6.37 \times 10^{10} m)$
                                 $v = 4.63 \times 10^2 m/s$
คำตอบ อัตราเร็วเชิงเส้นของวัตถุที่อยู่บนเส้นศูนย์สูตร 463 เมตรต่อวินาที

หาขนาดของความเร่งสู่ศูนย์กลางของวัตถุที่อยู่บนเส้นศูนย์สูตรของโลก
จาก                        $a_c = \omega ^2 r$
แทนค่า                   $v = (7.27\times 10^{- 5} rad/s) \times (6.37 \times10^{10} m)$
                               $a_c = 3.37 \times 10^{ - 2} m/s^2$
คำตอบ     ขนาดของความเร่งสู่ศูนย์กลางของวัตถุที่อยู่บนเส้นศูนย์สูตรของโลกเท่ากับ   $displaystyle 3.37 \times 10^{ - 2} m/s^2$
หมายเหตุ   จากตัวอย่าง 4.8 จะเห็นว่าวัตถุที่อยู่บนผิวโลกมีความเร่งสู่ศูนย์กลาง ดังนั้น  กรอบอ้างอิงที่อยู่บนผิวโลกจึงไม่ใช่กรอบอ้างอิงเฉื่อยที่แท้จริง แต่เราประมาณว่าเป็นกรอบอ้างอิงเฉื่อย

การเคลื่อนที่ของดาวเทียม
ดาวเทียมที่โคจรรอบโลกมีเป็นจำนวนมาก ดาวเทียมแต่ละดวงจะทำหน้าที่ต่างๆ กัน เช่น ดาวเทียมอุตุนิยมดาวเทียมสำรวจทรัพยากร ดาวเทียมสื่อสารและดาวเทียมจารกรรมททางทหารเป็นต้น ดาวเทียมแต่ละดวงมีรัศมีวงโคจรต่างกันแต่ต่างก็เคลื่อนที่รอบโลกในแนววงกลม โดยมีแรงที่โลกดึงดูดดาวเทียมเป็นแรงสู่ศูนย์กลางกระทำต่อดาวเทียม ดาวเทียมแต่ละดวงจะเคลื่อนที่รอบโลกด้วยอัตราเร็วอย่างไร

การเคลื่อนที่ของดาวเทียมรอบโลก

จากรูป ดาวเทียมมวล m โคจรรอบโลกด้วยอัตราเร็ว v ณ ตำแหน่งวงโคจรซึ่งห่างศูนย์กลางของโลกเป็นระยะ r ให้ M เป็นมวลของโลก F_c

เป็นแรงสู่ศูนย์กลางซึ่งเป็นแรงดึงดูดที่โลกกระทำกับดาวเทียม และหาค่าของแรงนี้ได้จากกฎแรงดึงดูดระหว่างของนิวตัน
                                            $F=\frac{{GMm}}{{r^2}}$
                                        ดังนั้น $\frac{{mv^2}}{r}=\frac{{GMm}}{{r^2}}$
                   $v^2 = \frac{{GM}}{r}$                                                  (4.12)
       จากสมการ (4.12) จะเห็นว่า ดาวเทียมที่มีรัศมีวงโคจรต่างกันจะเคลื่อนที่ด้วยอัตราเร็วเชิงเส้นต่างกันด้วย
       การส่งดาวเทียมขึ้นไปสู่วงโคจรต่างๆ รอบโลกนั้น ได้มีการกำหนดรัศมีวงโคจรไว้ก่อน แล้วคำนวณหาแรงสู่ศูนย์กลางที่กระทำกับดาวเทียมและอัตราเร็วเชิงเส้นในวงโคจรนั้นๆ เมื่อยิงดาวเทียมขึ้นไปจนมีความสูงหรือรัศมีของการโคจรตามต้องการแล้ว จึงปรับทิศทางและอัตราเร็วของดาวเทียมเพื่อให้เข้าสู่วงโคจรรอบโลกตามที่กำหนดไว้
        เมื่อสังเกตดาวเทียมสื่อสารจากพื้นโลก จะเห็นดาวเทียมสื่อสารอยู่ ณ ตำแหน่งเดิมตลอดเวลา ที่เป็นเช่นนี้ เพราะดาวเทียมสื่อสารมีคาบของการโคจรรอบโลกเท่ากับคาบการหมุนของโลกรอบตัวเอง หรืออัตราเร็วเชิงมุมของดาวเทียมสื่อสารเท่ากับอัตราเร็วเชิงมุมในการหมุนรอบตัวเองของโลก และการที่ดาวเทียมสื่อสารอยู่ที่ตำแหน่งเดิมโดยไม่เปลี่ยนแปลง ทำให้สถานีภาคพื้นดินและดาวเทียมสามารถติดต่อกันได้ตลอดเวลา
        ตัวอย่าง 7 โลกหมุนรอบตัวเองเท่ากับ 24 ชั่วโมง รัศมีวงโคจรรอบโลกของดาวเทียมสื่อสารจะต้องเป็นเท่าใดและมีอัตราเร็วเชิงมุมเท่าใด กำหนดให้ $G = 6.67 \times 10^{ - 11}$ นิวตัน เมตร² ต่อกิโลกรัม² มวลของโลก5.95 x 10²⁴กิโลกรัม
    วิธีทำ
                     เนื่องจากคาบของดาวเทียมสื่อสารเท่ากับคาบของการหมุนรอบตัวเองของโลก
                     จาก                      $\omega = \frac{{2\pi }}{T}$
                                    ในที่นี้              T      =     86,400 s
                         แทนค่า                          $\omega = 7.27 \times 10^{ - 5} rad/s$
                     จาก                                 $v^2 = \frac{{GM}}{r}$
                        และ                                 $v = \omega r$
                     จะได้                               $r^3 = \frac{{GM}}{{\omega ^2 }}$
                     แทนค่า                             $r^3 = 74848.19 \times 10^{18}$
                                           $r = 42.14 \times 10^6 m$
  คำตอบ รัศมีวงโคจรรอบโลกของดาวเทียมเท่ากับ $42.14 \times 10^6$ เมตร
            อัตราเร็วเชิงมุมของดาวเทียมสื่อสารเท่ากับ $7.26 \times 10^{ - 5}$ เรเดียน/วินาที

โจทย์เกี่ยวกับการเคลื่อนแบบวงกลม